
PRML - Lab 3: 聚类算法
本次作业利用 NumPy 实现了一个 K-Means 模型和一个 GMM 模型,并利用 Gap Statistic 方法实现了数据集中聚簇数量的自动推测。
Pattern Recognition and Machine Learning (H) @ Fudan University, spring 2021.
实验简介
实验报告
1 K-Means 模型
1.1 算法思路
K-Means 模型的算法思路很简单,具体训练过程如下:
- 给定 $k$ 值(需要将数据集聚成几个簇),初始时随机选择 $k$ 个聚簇中心。
- 将每个数据点分配给距离最近的聚簇中心。
- 修正聚簇中心为本次分配到此聚簇中心的数据点的中心点(平均值)。
- 重复以上步骤,直到满足终止条件。这里我们选择的终止条件是「没有数据点的标签(即分配到的聚簇中心)再发生变化」,当然也可以设置为其他合理的终止条件。
预测时,我们选择距离数据点最近的聚簇中心,作为数据点所属的聚簇。
例如对于一个随机生成的数据集,我们利用 K-Means 模型将其分为 3 类的结果如下:
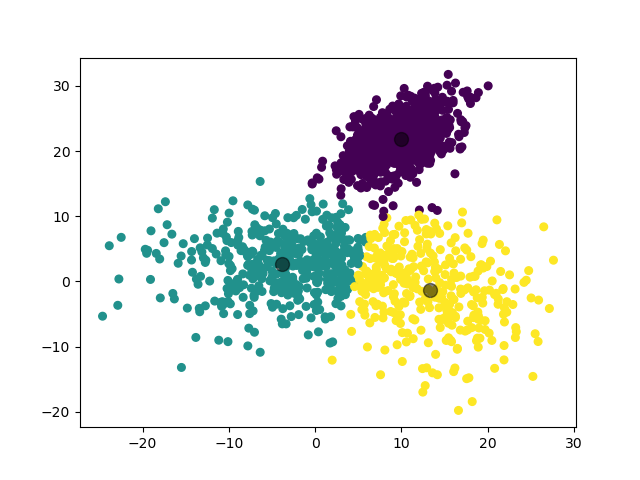
1.2 一些优化
K-Means 模型的一个问题是,由于初始时的聚簇中心是随机选择的,如果选择得不好,可能会导致收敛到局部最优解而非全局最优解。例如对于同样的数据集,可能生成如下的聚类结果:
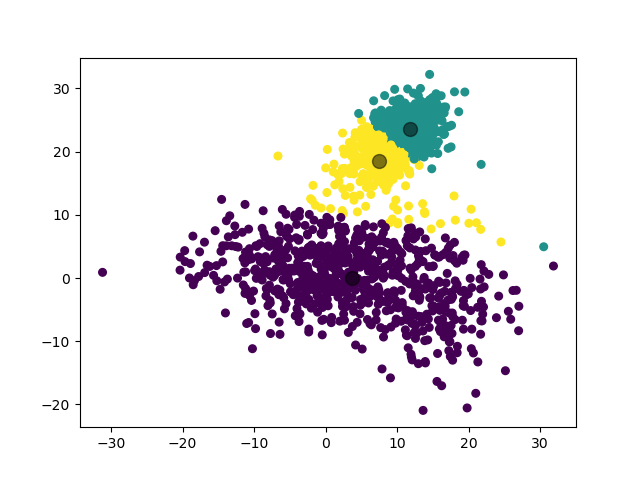
作为优化,我们参考 scikit-learn 库的思路,对于同样的训练数据,使用不同的随机种子训练 $n$ 次(本实验中默认取 $10$,可通过参数 n_epochs 调整),最后选择最优的训练模型作为预测时使用的模型。这里我们对最优的判断标准是各簇内距离(各数据点到聚簇中心距离)的平方和最小。具体来说,即要求如下参数的值最小:
$$ W = \sum_{\mathbf{x}_i\in \mathbf{D}} \sum_{\mathbf{c}_k\in \mathbf{C}} (\mathbf{x}_i - \mathbf{c}_k)^2 $$
其中 $\mathbf{x}_i$ 为数据点,$\mathbf{D}$ 为数据集,$\mathbf{c}_k$ 为聚簇中心,$\mathbf{C}$ 为聚簇中心集。
经实验,对于一般的数据集,这个优化可以有效地使 K-Means 模型收敛到全局最优解。
1.3 基础实验
1.3.0 生成数据集
我们利用以下函数生成数据集:
|
|
对于一维的情形,我们使用 numpy 库提供的函数 random.default_rng().normal 和参数 mean, scale, size 从一维高斯分布中生成数据集。对于多维的情形,我们使用 numpy 库提供的函数 random.default_rng().multivariate_normal 和参数 mean, cov, size 从多维高斯分布中生成数据集。其中:
mean表示数据集的均值cov表示数据集的协方差(对于多维的情形)scale表示数据集的标准差(对于一维的情形)size表示数据集的大小
如此生成若干数据集后,我们将它们合并为一个大数据集,并对其进行打乱。其中 $80\%$ 作为训练集,$20\%$ 作为测试集。
1.3.1 实验 1
第一个实验,我们对 3 个二维高斯分布数据集进行聚类。
1.3.1.1 数据集参数
1.3.1.2 实验结果

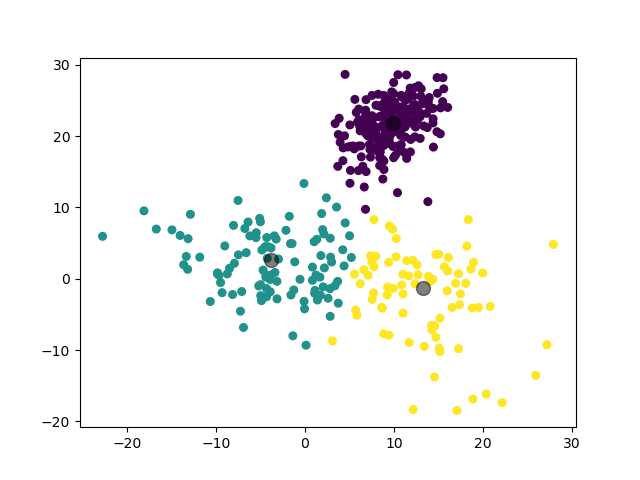
1.3.2 实验 2
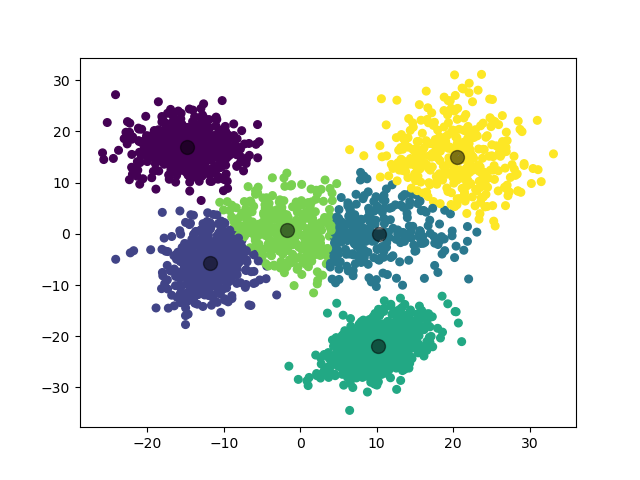
第二个实验,我们增加数据集的数量,对 5 个二维高斯分布数据集进行聚类。
1.3.2.1 数据集参数
1.3.2.2 实验结果
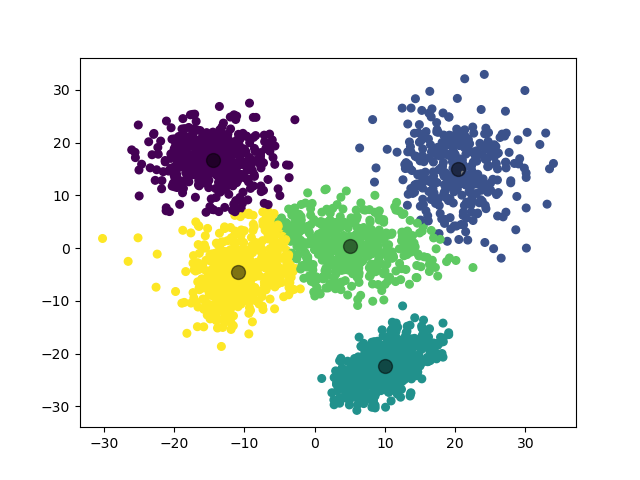
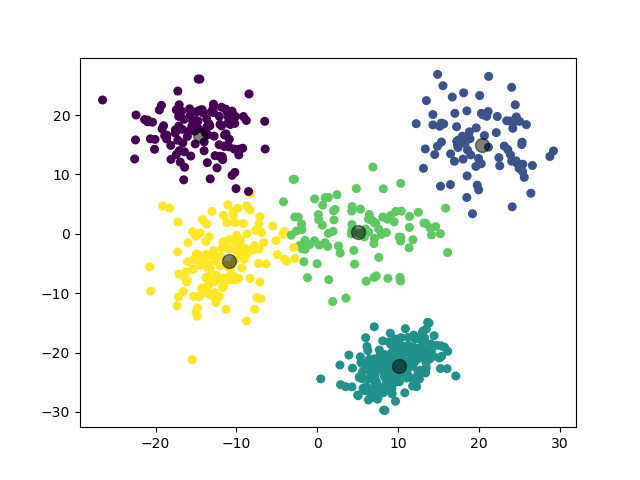
1.3.3 实验 3
第三个实验,我们提高数据集的维度,对 3 个三维高斯分布数据集进行聚类。
1.3.3.1 数据集参数
1.3.3.2 实验结果
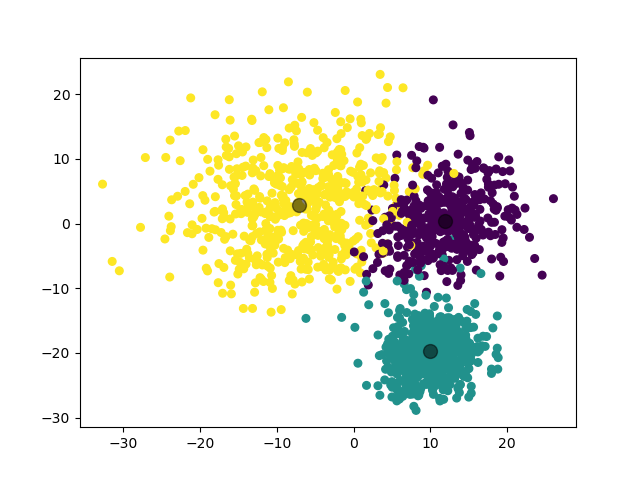
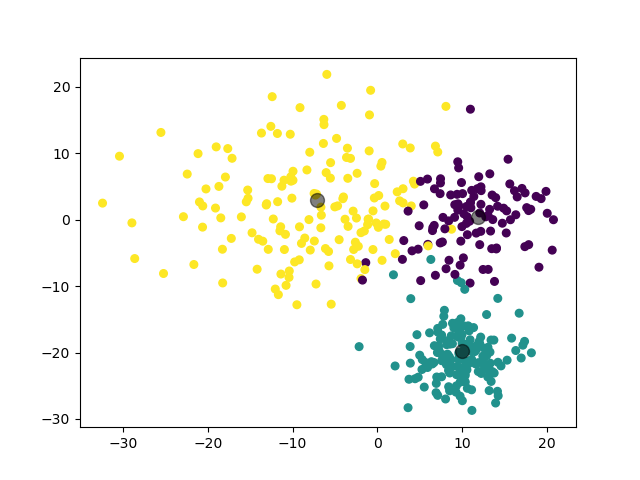
(图中为数据集在二维平面上的投影。)
1.3.4 实验 4
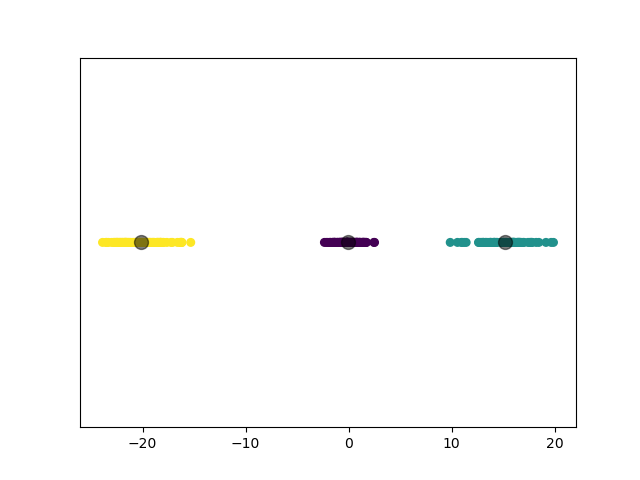
第四个实验,我们降低数据集的维度,对 3 个一维高斯分布数据集进行聚类。
1.3.4.1 数据集参数
1.3.4.2 实验结果
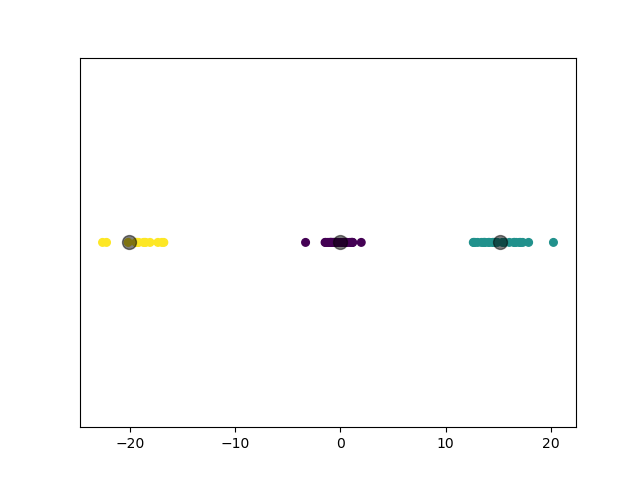
1.3.5 实验 5
第五个实验,为了与之后的 GMM 模型进行对比,我们对 3 个扁平形状的二维高斯分布数据集进行聚类。
1.3.5.1 数据集参数
1.3.5.2 实验结果
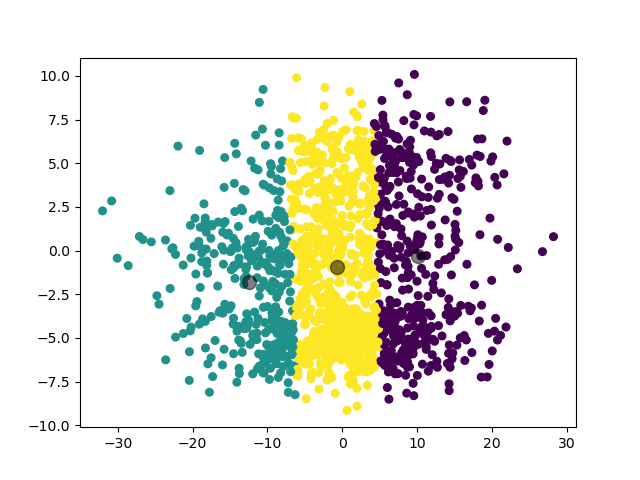
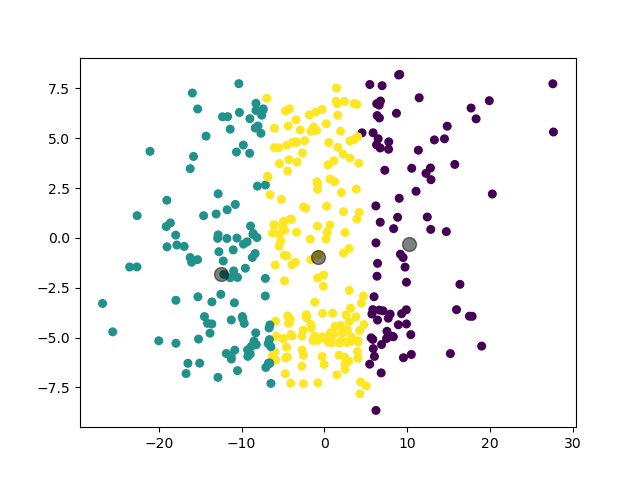
可见,对于这样的数据集,由于 K-Means 模型以距离为唯一参考标准的特性,其聚类结果并不是很理想。这也是为什么我们要引入 GMM 模型。
2 GMM 模型
2.1 算法思路
GMM 模型(Gaussian Mixture Model)的算法思路类似于 K-Means 模型,区别在于 GMM 模型不再以到聚簇中心的距离为参考标准,而是用 $k$ 个单一高斯分布的线性组合来拟合原数据集。我们将使用 EM 算法(Expectation-Maximization algorithm)进行迭代,具体训练过程如下:
-
给定 $k$ 值(需要将数据集聚成几个簇),初始化各个参数:
means:从数据集中随机选择 $k$ 个点,作为每个高斯分布的初始中心点。covs:对于多维的情形,初始化每个高斯分布的协方差为一个单位矩阵。scales:对于一维的情形,初始化每个高斯分布的标准差为 $1$。weights:初始化任一数据点被分配到每个聚簇的先验概率为 $1/k$。
-
EM 算法的 E(xpectation) 步骤:通过目前的参数计算每个数据点被分配到每个聚簇的概率。
先计算给定参数的高斯分布的概率密度函数。
对于多维的情形,
$${ p(\mathbf{x}) = \frac{1}{\sqrt{(2\pi)^d |\mathbf{\Sigma}_i|}} \exp(-\frac{1}{2}(\mathbf{x}-\mathbf{\mu}_i)^\mathrm{T} \mathbf{\Sigma}_i^{-1} (\mathbf{x}-\mathbf{\mu}_i)) }$$
其中 $i$ 表示第 $i$ 个聚簇,$d$ 表示数据点的维度,$\mathbf{\mu}$ 表示
means,$\mathbf{\Sigma}$ 表示covs。对于一维的情形,
$${ p(x) = \frac{1}{\sqrt{2\pi\sigma_i^2}} \exp(-\frac{(x-\mu_i)^2}{2\sigma_i^2}) }$$
其中 $i$ 表示第 $i$ 个聚簇,$\mu$ 表示
means,$\sigma$ 表示scales。然后利用 Bayes’ Theorem,计算每个数据点被分配到每个聚簇的概率
$${ f_i(\mathbf{x}) = \frac{p(\mathbf{x})\phi_i}{\sum\limits_{i=1}^k p(\mathbf{x})\phi_i} }$$
其中 $i$ 表示第 $i$ 个聚簇,$\phi$ 表示
weights,$k$ 表示 $k$ 值。 -
EM 算法的 M(aximization) 步骤:根据当前每个聚簇的概率矩阵,更新模型的各个参数。
-
means:$${ \mathbf{\mu}_i = \frac {\sum\limits_{i=1}^k(f_i(\mathbf{x})\cdot \mathbf{x})} {\sum\limits_{i=1}^k f_i(\mathbf{x})} }$$
-
covs:对于多维的情形,$${ \mathbf{\Sigma}_i = \frac {\sum\limits_{i=1}^k( f_i(\mathbf{x})\cdot (\mathbf{x}-\mathbf{\mu}_i)^\mathrm{T} (\mathbf{x}-\mathbf{\mu}_i) )} {\sum\limits_{i=1}^k f_i(\mathbf{x})} }$$
-
scales:对于一维的情形,$${ \sigma_i = \sqrt{ \frac {\sum\limits_{i=1}^k(f_i(x)\cdot (x-\mu_i)^2)} {\sum\limits_{i=1}^k f_i(x)} } }$$
-
weights:$${ \phi_i = \frac{1}{N} \sum\limits_{i=1}^k f_i(\mathbf{x}) }$$
-
-
重复 EM 算法,直到满足终止条件。GMM 模型的终止条件与 K-Means 模型一致。
预测时,对于每个数据点,我们根据每个聚簇的概率矩阵,选择概率最大的聚簇作为数据点所属的聚簇。
例如对于一个随机生成的数据集,我们利用 GMM 模型将其分为 3 类的结果如下:
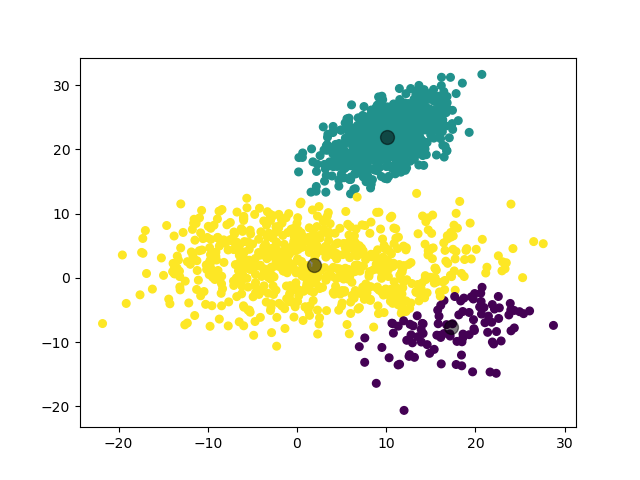
2.2 一些优化
与 K-Means 模型类似,GMM 模型初始时的聚簇中心也是随机选择的,因此这里我们采用了和 K-Means 模型一样的优化思路,即先使用不同的随机种子训练 $n$ 次,最后选择最优的训练模型作为预测时使用的模型。与 K-Means 模型不同的地方在于,在 GMM 模型中,我们不能简单地使用到聚簇中心的距离作为参考标准。实际上,我们希望每个数据点被分配到其所属的聚簇时,其在概率矩阵中对应的概率尽可能大。因此,这里我们对最优的判断标准是要求如下参数的值最大:
$$ \sum\limits_{i=1}^N \max_{1\le j\le k}{\{f_j(\mathbf{x})\}} $$
经实验,这个优化也可以有效地使 GMM 模型收敛到全局最优解。
2.3 基础实验
2.3.0 生成数据集
这里我们使用与 K-Means 相同的数据集生成方法。
2.3.1 实验 1
第一个实验,我们对 3 个二维高斯分布数据集进行聚类。
2.3.1.1 数据集参数
2.3.1.2 实验结果

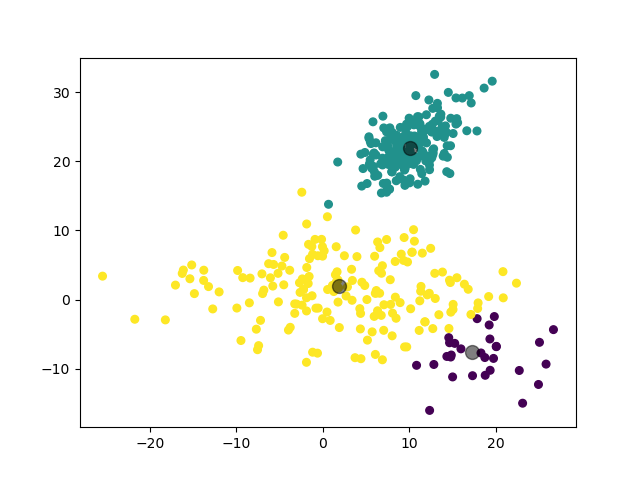
2.3.2 实验 2
第二个实验,我们对 5 个二维高斯分布数据集进行聚类。
2.3.2.1 数据集参数
2.3.2.2 实验结果
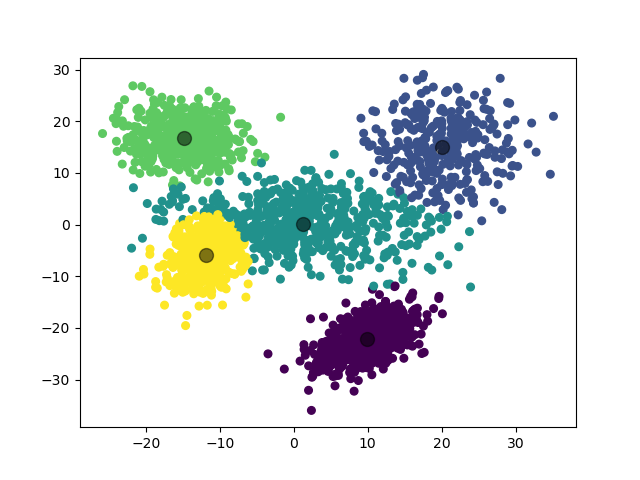
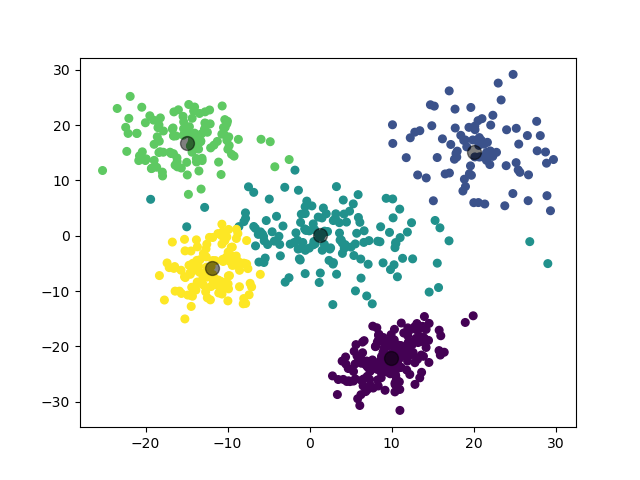
2.3.3 实验 3
第三个实验,我们对 3 个三维高斯分布数据集进行聚类。
2.3.3.1 数据集参数
2.3.3.2 实验结果
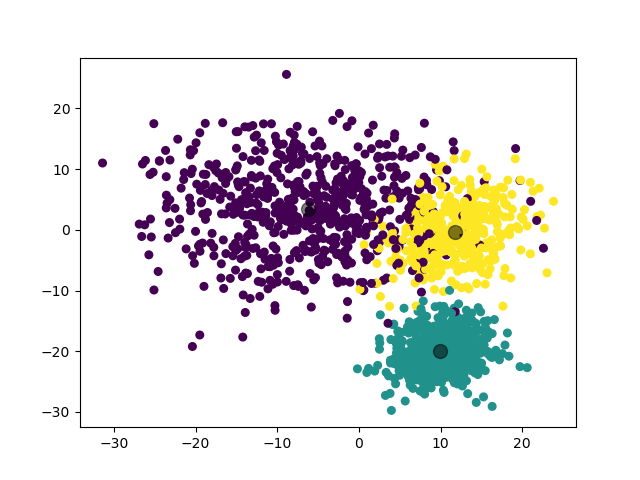
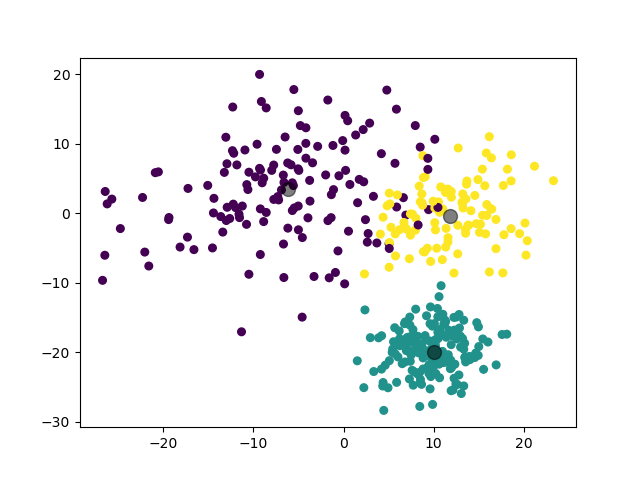
(图中为数据集在二维平面上的投影。)
2.3.4 实验 4
第四个实验,我们对 3 个一维高斯分布数据集进行聚类。
2.3.4.1 数据集参数
2.3.4.2 实验结果
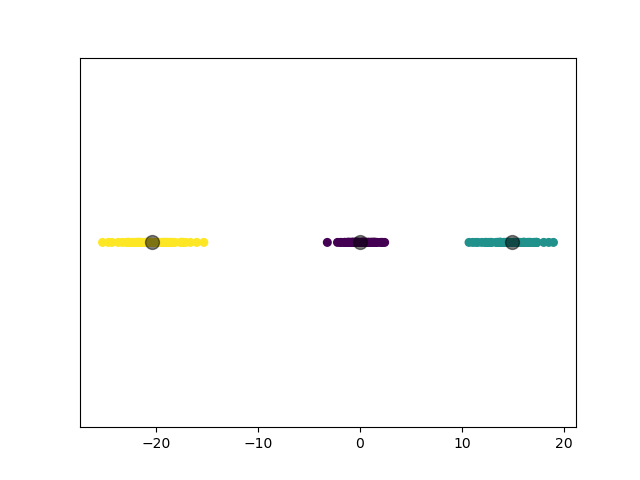
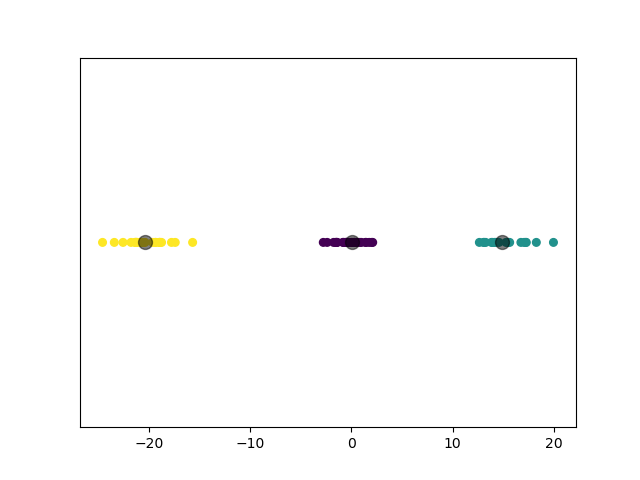
2.3.5 实验 5
第五个实验,我们对 3 个扁平形状的二维高斯分布数据集进行聚类。
2.3.5.1 数据集参数
2.3.5.2 实验结果
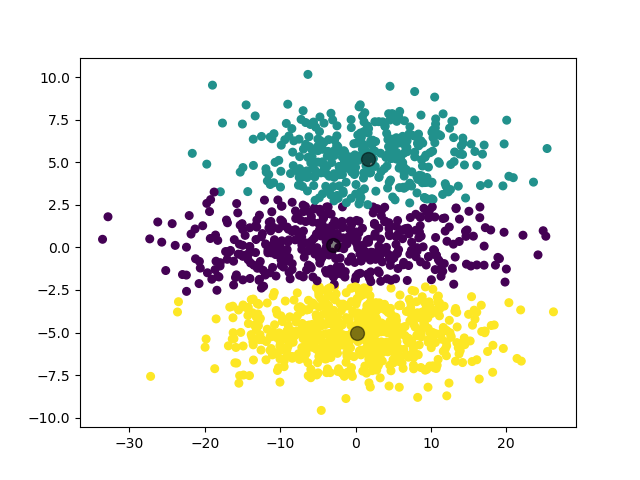
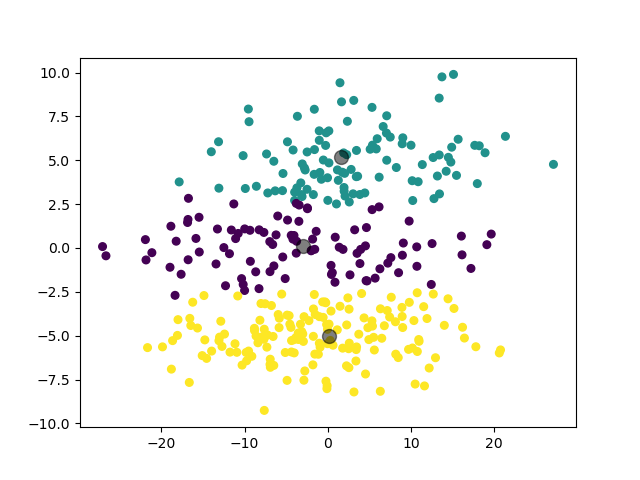
可见,GMM 模型对于高斯混合分布数据集,其聚类结果比 K-Means 模型更加准确。
3 自动选择聚簇数量
3.1 算法思路
这里我们利用 Gap Statistic 方法实现了数据集中聚簇数量的自动推测。Gap Statistic 方法的思想是:对于数据集聚类结果的簇内距离,它和同规模均匀分布的期望簇内距离相比,两者的差距越大,则认为模型的聚类结果越好,即 $k$ 值的选择越好。具体来说,即希望如下参数的值尽可能大:
$$ \mathrm{Gap}_k = \operatorname{E}(\log {W’}_k) - \log W_k $$
其中,$k$ 即选择的 $k$ 值,$W_k$ 为数据集 $\mathbf{D}$ 聚类结果的簇内距离的平方和,${W’}_k$ 为同规模均匀分布 $\mathbf{U}$ 聚类结果的簇内距离的平方和。这里 $W$ 的具体定义参见 1.2 节。
我们利用 Monte Carlo 方法计算 $\operatorname{E}(\log {W’}_k)$ 的值。我们在数据集 $\mathbf{D}$ 覆盖的矩形范围内进行 $B$ 次随机均匀采样,得到 $B$ 个不同的 ${W’}_k^{(b)}$,于是我们有
$$ \operatorname{E}(\log {W’}_k) = \frac{1}{B} \sum\limits_{b=1}^B \log {W’}_k^{(b)} $$
我们的算法底层建立在 K-Means 模型的基础上。实验时,需指定扫描时的最大 $k$ 值 $k_{\max}$,模型将在 $[1,k_{\max}]$ 的范围内找到使得 $\mathrm{Gap}_k$ 最大的 $k$ 值,作为推测的数据集中的聚簇数量。
3.2 一些优化
为了一定程度上减少扫描时间,我们设定了一个终止阈值 $B$(默认取 $3$,可通过参数 break_threshold 调整)。当 $\mathrm{Gap}_k$ 连续 $B$ 次没有增长时,我们就认为已经找到了最优的 $k$ 值,模型自动终止扫描。
3.3 基础实验
3.3.0 生成数据集
这里我们使用与 K-Means 相同的数据集生成方法。
3.3.1 实验 1
第一个实验,我们对 3 个二维高斯分布数据集进行聚类。
3.3.1.1 数据集参数
3.3.1.2 实验结果
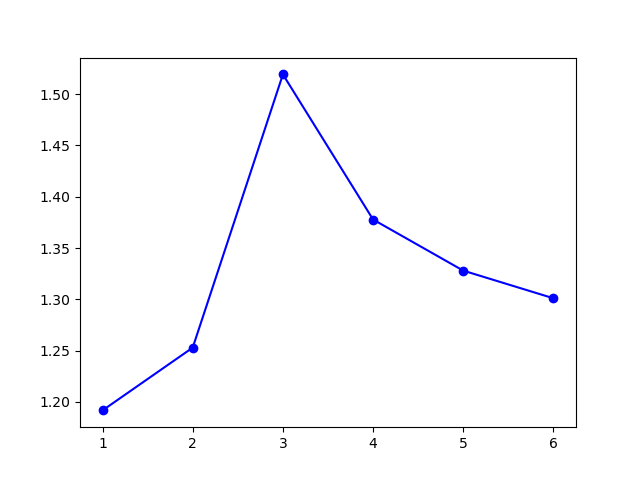
模型选择的 $k$ 值为 $3$,聚类结果:
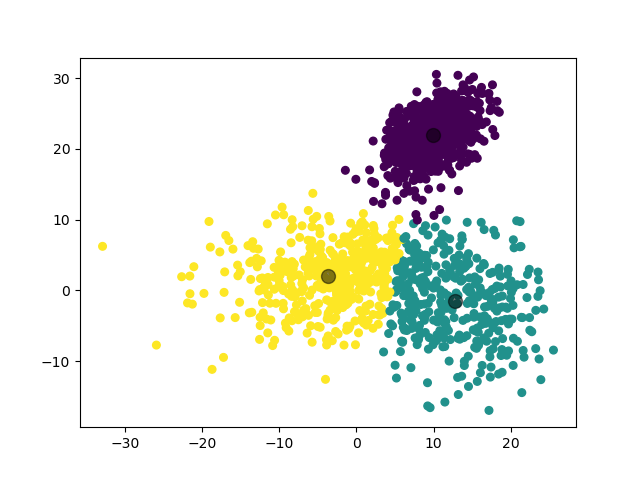
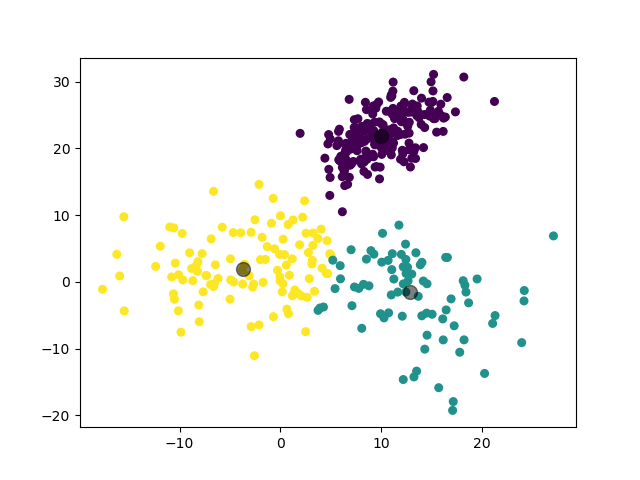
3.3.2 实验 2
第二个实验,我们对 5 个二维高斯分布数据集进行聚类。
3.3.2.1 数据集参数
3.3.2.2 实验结果
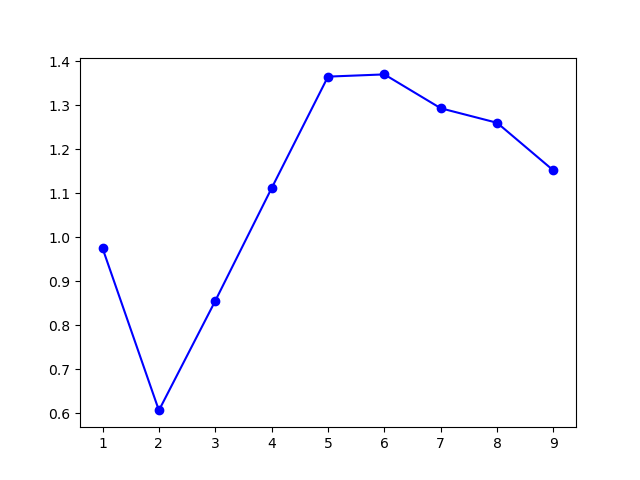
模型选择的 $k$ 值为 $6$,聚类结果:
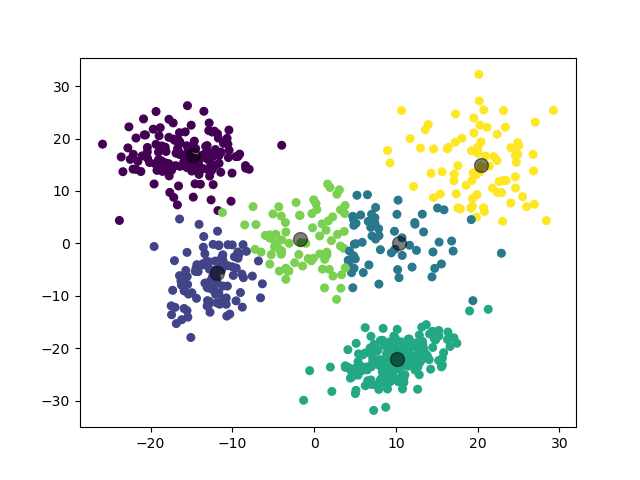
虽然实际上应当是 $5$ 个高斯分布,不过考虑到模型在 $k=5$ 和 $k=6$ 处取得了接近的 $\mathrm{Gap}$ 值,这个聚类结果也是可以理解的。
3.3.3 实验 3
第三个实验,我们对 3 个三维高斯分布数据集进行聚类。
3.3.3.1 数据集参数
3.3.3.2 实验结果
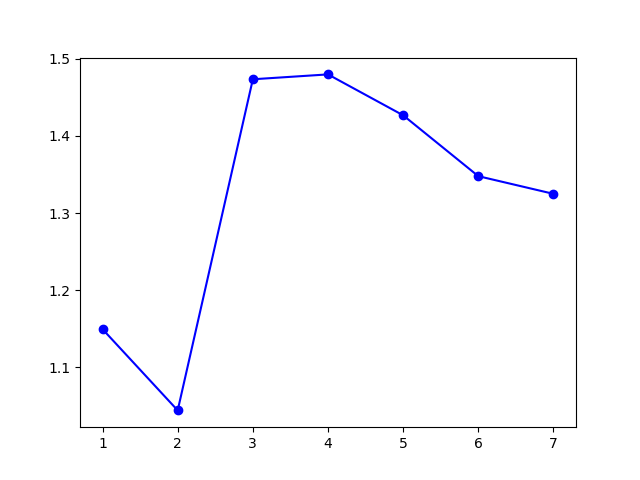
模型选择的 $k$ 值为 $4$,聚类结果:
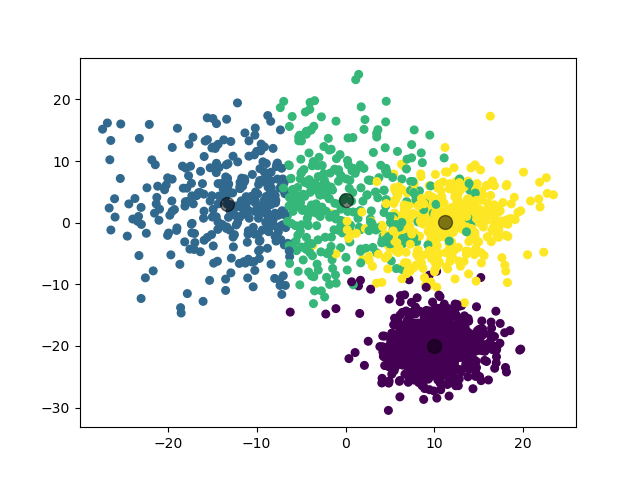
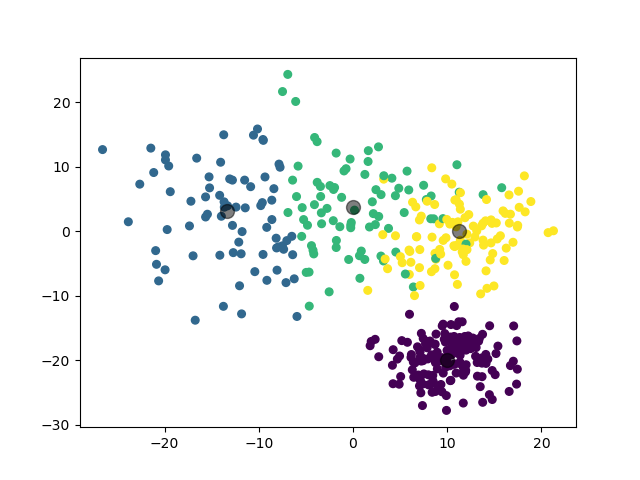
(图中为数据集在二维平面上的投影。)
类似地,模型在 $k=3$ 和 $k=4$ 处取得了接近的 $\mathrm{Gap}$ 值,说明这两个 $k$ 值都是可以接受的。
3.3.4 实验 4
第四个实验,我们对 3 个一维高斯分布数据集进行聚类。
3.3.4.1 数据集参数
3.3.4.2 实验结果
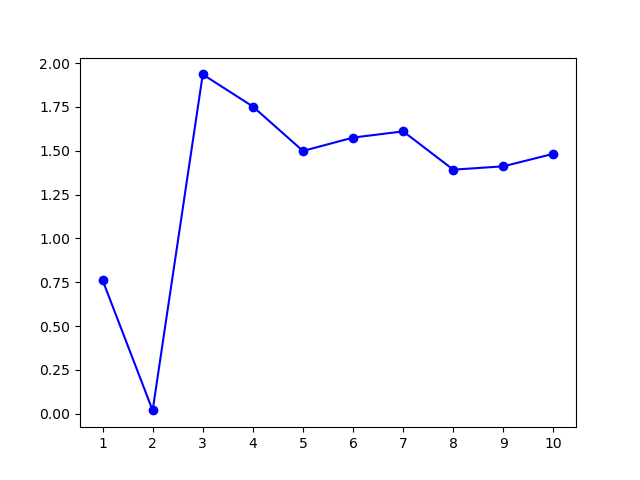
模型选择的 $k$ 值为 $3$,聚类结果:
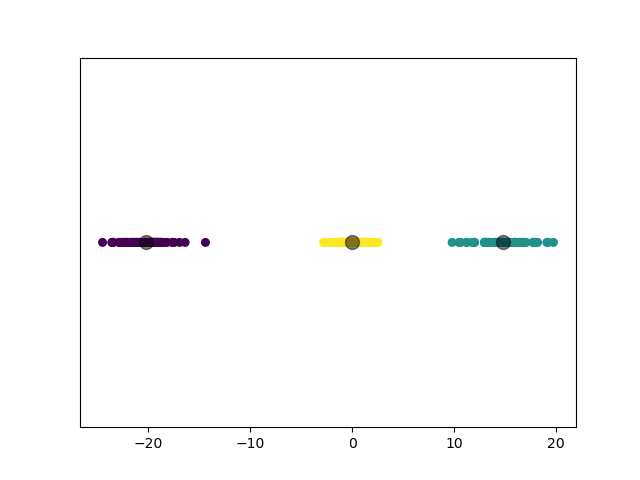
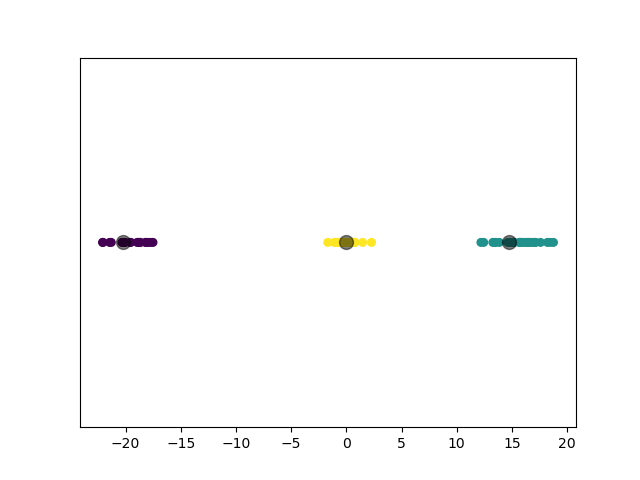
3.3.5 实验 5
第五个实验,我们对 3 个扁平形状的二维高斯分布数据集进行聚类。
3.3.5.1 数据集参数
3.3.5.2 实验结果
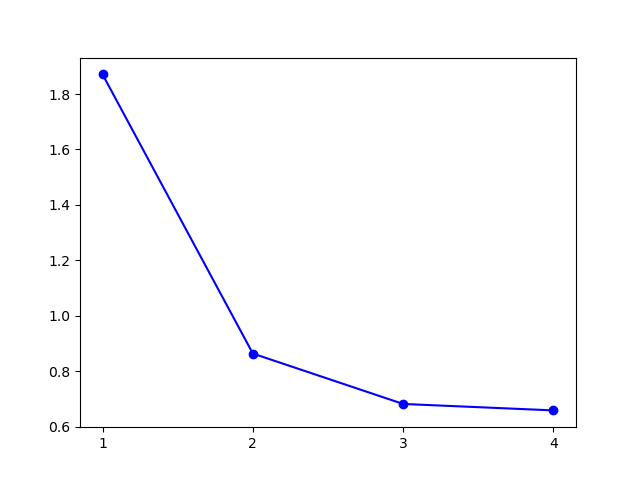
模型选择的 $k$ 值为 $1$,聚类结果:
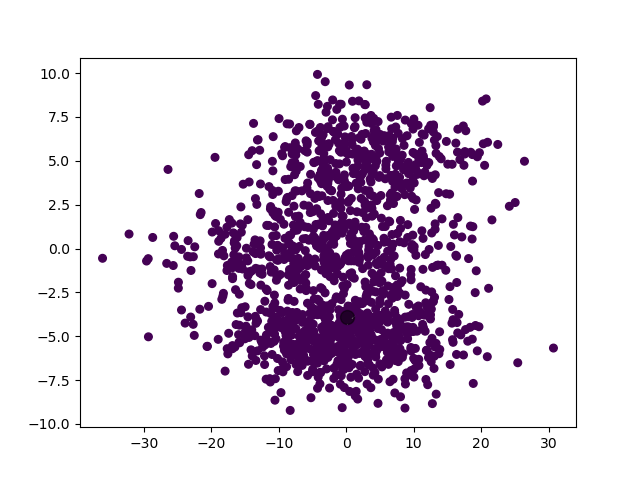
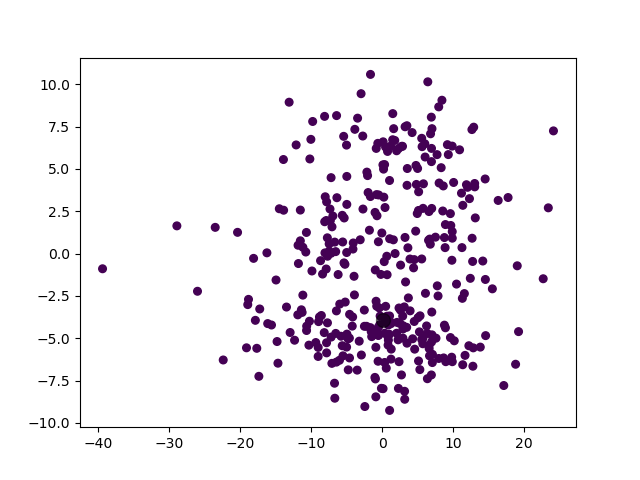
实际上,从人类的视角来看,这个聚类结果也是可以理解的。
4 运行代码
执行以下命令进行模型的训练及预测。
|
|
生成数据集使用的参数可以在 TestSuite 类中进行调整。