
DSP - Lab 3: MFCC: Mel 频率的倒谱系数
本实验中,我们实现了一个端点检测算法,并构造了一个 Mel 滤波器组处理信号的能量谱,最后利用离散余弦变换(DCT)得到了信号的 MFCC 系数。
Digital Signal Processing @ Fudan University, fall 2021.
实验简介
- 录音,用 8 kHz 采样,朗读单词 shop。
- 端点检测(画出语音波形,标出起点和终点)。
- 从语音起点开始取 $L$ 个窗口,窗度为 $N$,窗口重叠 $N/2$。
- 每一个窗口,计算 MFCC 系数(维度为 $D$)。用表格列出 $L$ 个 $D$ 维 MFCC 系数。
注意:参数 $L$, $N$, $D$ 请合理设定。
实验报告
1 预加重
在载入音频后,我们需要先进行一些预处理,这里主要是进行了预加重(pre-emphasis)和归一化。其中预加重的目的是为了补偿输入信号中的高频分量,这是因为在信号的传输过程中,信号频率越高,能量衰减越大。由于预加重并不影响噪声,因此预加重可以有效提高信号的整体信噪比。
预加重的计算方法如下:
$$y(n) = x(n)-\alpha x(n-1)$$
其本质就是一个 $H(z) = 1-\alpha z^{-1}$ 的高通滤波器,其中系数 $\alpha$ 在本实验中的取值为 $0.97$。
2 端点检测
接下来我们将音频中的语音部分提取出来,在这一步我们将确定语音的起点和终点。其基本原理是利用语音的短时平均幅度和短时过零率(Zero-Crossing Rate, ZCR)。
2.1 分帧计算短时平均幅度和短时过零率
首先将信号分帧,同之前讲过的 STFT 过程,这里不再赘述。
分帧后,我们就可以计算每帧的平均幅度 $\overline{M_i}$ 和过零率 $\overline{Z_i}$ 了。
平均幅度:
$$\overline{M_i} = \frac{1}{N} \sum\limits_{n=i}^{i+N-1} |S(n)|$$
其中 $N$ 为窗口宽度,$S$ 为信号幅度。本实验中 $N$ 的取值为 $128$。
|
|
过零率:
$$\overline{Z_i} = \frac{1}{2T} \sum\limits_{n=i+1}^{i+N-1} |\operatorname{sgn}S(n)-\operatorname{sgn}S(n-1)|$$
其中 $T$ 为窗口时间宽度,$\operatorname{sgn}$ 为符号函数。本实验中 $T$ 的取值为 $16\ \mathrm{ms}$。
2.2 利用短时平均幅度(高阈值)初步判断区间
|
|
第一步,我们顺序遍历所有帧,将所有短时平均幅度高于阈值 $M_H$ 的区间提取出来。这里进行了一个区间重叠判断,如果当前帧和上一帧的间距不超过 2,则判定重叠,将当前帧并入上一个区间。本实验中 $M_H$ 的取值为 $0.6\%$。
通过这一步,我们至少可以找到信号中所有的浊音。不过对于测试音频 shop 来说,浊音 -o- 和清音 -p 之间存在一个小的间隔,且清音 -p 的持续时间很短,这可能导致清音 -p 无法被检测到。因此这里将阈值 $M_H$ 设置得比较低,目的是为了在这一步能同时检测到幅度较小的清音,但副作用是如果背景噪声较大,可能会影响端点检测的结果。
2.3 利用短时平均幅度(低阈值)扩展区间
|
|
第二步,我们对上一步得到的区间进行扩展,分别向前和向后查找新的起点和终点。当短时平均幅度降低到阈值 $M_L$ 以下时,即可确定新的端点。这里采用了和第一步类似的区间重复判断。本实验中 $M_L$ 的取值为 $0.2\%$。
通过这一步,我们基本利用平均幅度的信息找到了语音段的大致区间。不过由于清音段的幅度较小,难以与无声段区分,因此为了得到更精确的端点位置,我们需要利用清音段相较无声段过零率显著更高的特点。
2.4 利用短时过零率扩展区间
|
|
第三步,我们进一步扩展区间,这一步主要是为了精确判断清音段和无声段的分界点。观察信号的过零率曲线:
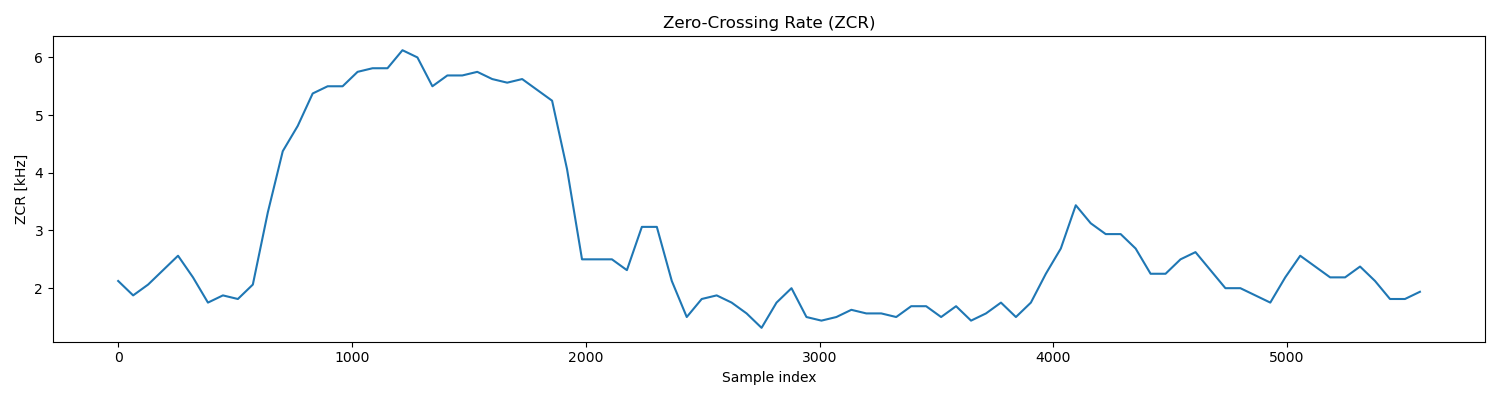
可见,无声情况下的短时过零率均值在 $2.0\ \mathrm{kHz}$ 左右,而清音段的短时过零率均值则在 $6.0\ \mathrm{kHz}$ 左右,因此不妨将过零率阈值 $Z_0$ 设置为 $4.5\ \mathrm{kHz}$。类似第二步,分别向前和向后查找,当短时过零率降低到阈值 $Z_0$ 以下时,即可确定新的端点。
通过这一步,我们就确定了语音段的范围。
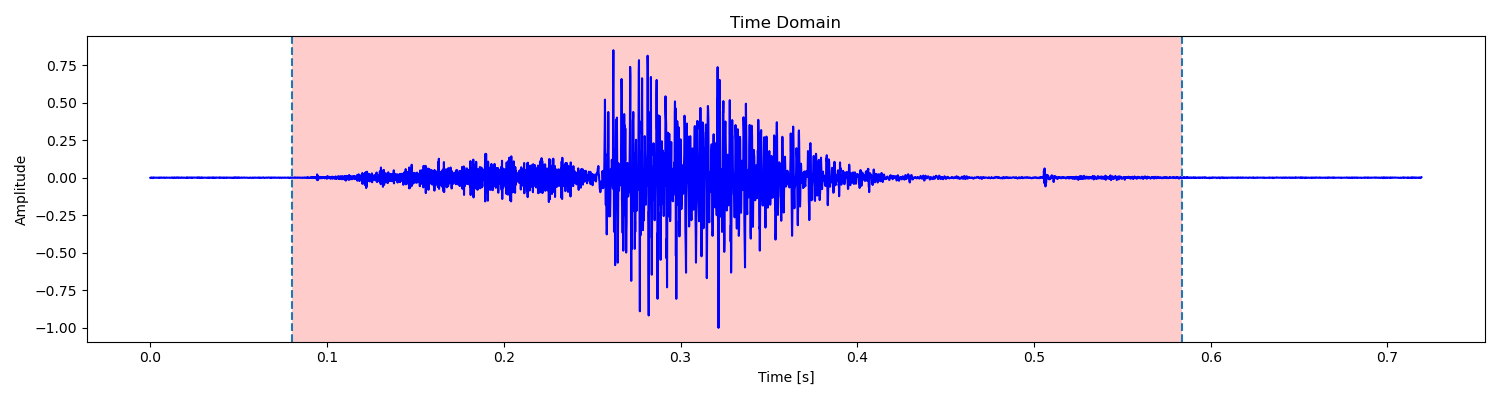
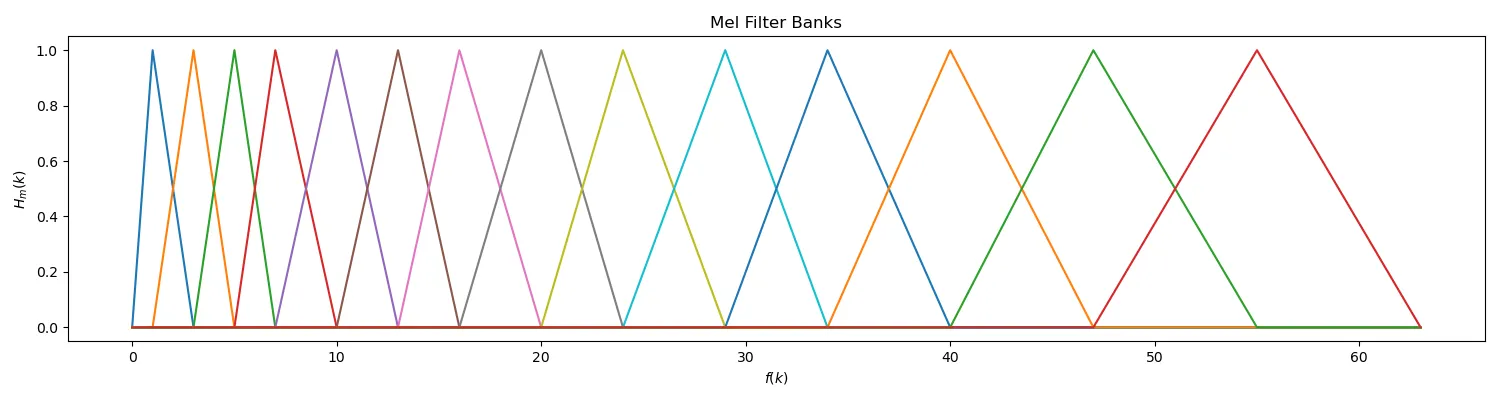
3 构造 Mel 滤波器组
基于人耳的听觉特性,我们可以构造 Mel 滤波器组来模拟人耳对声音的非线性感知。具体来说,Mel 频率与实际频率的对应关系如下:
$$ \begin{align*} B(f) &= 2595\log_{10}(1+\frac{f}{700}) \\ B^{-1}(f_{\mathrm{mel}}) &= 700\cdot (10^{f_{\mathrm{mel}}/2595}-1) \end{align*} $$
因此,首先我们将实际频域映射到 Mel 频域。这里我们取频域下限 $f_{\min}$ 为 $20\ \mathrm{Hz}$,也就是人类能听到的最低频率;取频域上限 $f_{\max}$ 为 $4000\ \mathrm{Hz}$,也就是采样频率 $f_s$ 的一半(由 Nyquist 定理可知)。
然后在 Mel 频域等间隔地取 $M$ 个滤波器的中心频率 $f_{\mathrm{c}}(m)$,再映射回实际频域,并转换为 FFT 频率点的位置 $f(m)$,有
$$f(m) = \frac{N}{f_s} B^{-1}(B(f_{\min}) + \frac{m}{M+1}(B(f_{\max})-B(f_{\min})))$$
其中 $N$ 为窗口宽度,$f_s$ 为采样频率。本实验中 $M$ 的取值为 $14$。
得到各 Mel 滤波器的中心频率后,我们就可以构造这 $M$ 个滤波器了。Mel 滤波器是具有三角形状的带通滤波器,其频率响应定义为:
$$ H_m(k) = \begin{cases} 0 &k < f(m-1) \\ \large \frac{k-f(m-1)}{f(m)-f(m-1)} &f(m-1) \le k \le f(m) \\ \large \frac{f(m+1)-k}{f(m+1)-f(m)} &f(m) < k \le f(m+1) \\ 0 &k > f(m+1) \end{cases} $$
如此我们就得到了 Mel 滤波器组。
4 使用 Mel 滤波器组处理能量谱
|
|
然后我们就可以使用这个 Mel 滤波器组处理信号的能量谱。这里能量谱就是频谱的平方,频谱的生成方法可参见上一个实验报告。
处理前的对数频谱图:
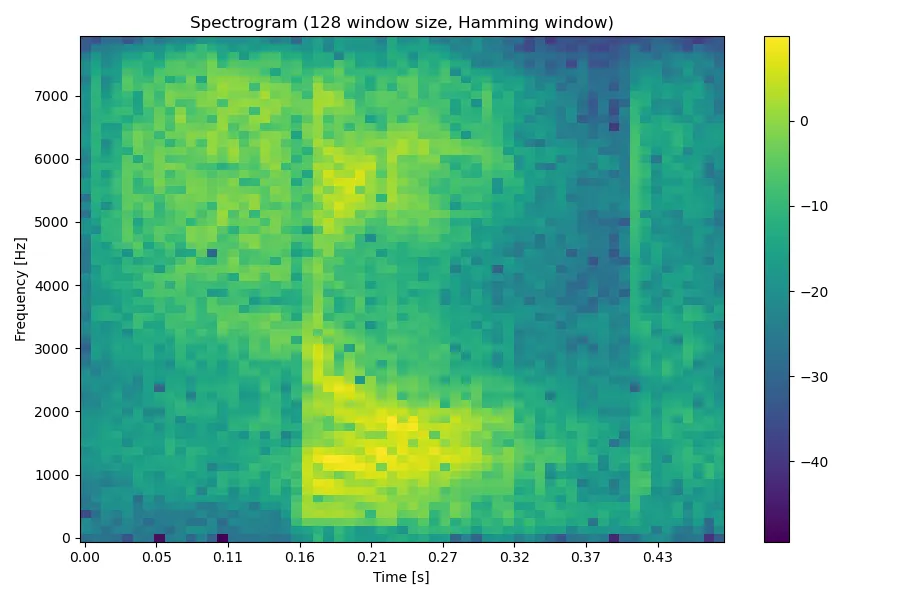
处理后的对数能量谱:
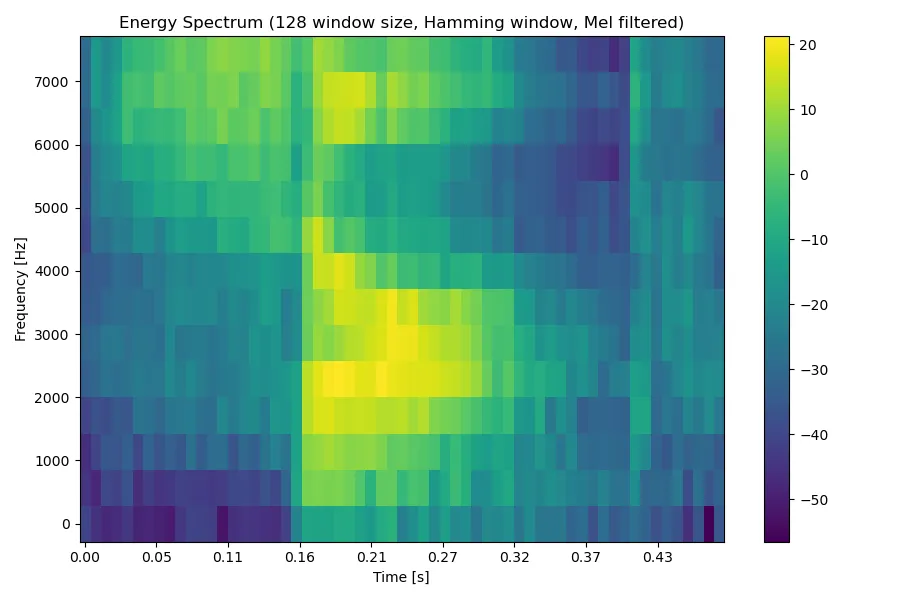
5 生成 MFCC 系数
最后,我们对刚才得到的对数能量谱使用离散余弦变换(Discrete Cosine Transform, DCT),就可以得到 Mel 频率的倒谱系数(Mel-Frequency Cepstral Coefficient, MFCC)。其中 DCT 的计算方法如下:
$$ \begin{align*} F(0) &= \frac{1}{\sqrt{M}} \sum\limits_{x=0}^{M-1} f(x) &u=0 \\ F(u) &= \sqrt{\frac{2}{M}} \sum\limits_{x=0}^{M-1} f(x)\cos(\frac{\pi u}{2M}(2x+1)) &u=1,2,…,D-1 \end{align*} $$
其中 $M$ 为 Mel 滤波器的个数,$D$ 为 MFCC 的维度。本实验中 $D$ 的取值为 $13$,即取计算结果的 $0$ ~ $12$ 阶 MFCC。
|
|
最终生成的 MFCC 如下所示(窗口总数 $L=61$,窗口宽度 $N=128$,MFCC 维度 $D=13$):
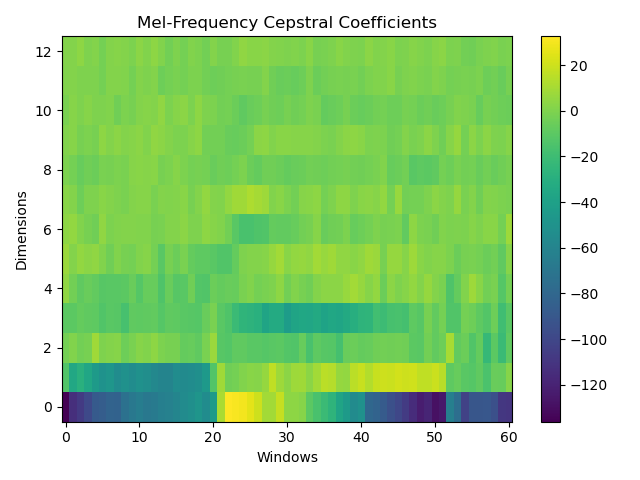
| 窗口 \ 阶数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | -136.184 | -13.031 | -2.768 | -10.172 | 4.658 | 7.187 | 3.683 | 2.385 | -0.476 | 0.321 | -1.567 | 0.348 | 1.143 |
| 2 | -113.156 | -35.058 | 0.548 | -10.253 | -3.016 | 1.534 | 4.940 | 1.142 | -2.413 | 2.069 | 2.118 | 1.584 | 1.352 |
| 3 | -107.730 | -29.099 | -3.024 | -7.169 | -8.689 | 4.982 | 0.501 | -4.845 | -6.363 | -2.063 | -0.074 | 0.039 | 3.631 |
| 4 | -98.901 | -36.441 | -2.307 | -8.584 | -6.138 | 3.381 | -1.805 | -0.057 | -4.116 | -0.884 | 1.934 | 0.269 | -0.232 |
| 5 | -88.325 | -44.003 | 8.463 | -8.954 | -8.032 | 4.853 | -3.866 | -0.217 | -5.332 | -2.305 | 0.061 | 0.164 | 1.579 |
| 6 | -86.533 | -50.468 | -0.195 | -13.077 | -11.467 | 0.751 | 4.591 | 2.563 | -1.104 | 4.104 | -0.182 | -2.775 | -2.728 |
| 7 | -82.730 | -47.477 | 1.002 | -10.279 | -10.261 | -3.788 | -0.606 | 1.254 | -2.126 | 1.093 | 0.833 | 1.140 | 1.035 |
| 8 | -83.094 | -54.283 | 2.142 | -11.372 | -10.434 | 0.357 | 0.665 | -0.255 | -0.374 | 3.381 | -4.290 | 1.005 | 2.238 |
| 9 | -73.489 | -50.941 | -4.853 | -16.360 | -9.717 | -1.993 | 0.968 | -1.636 | -1.547 | 1.331 | -0.682 | 0.714 | 1.014 |
| 10 | -68.593 | -54.086 | -1.231 | -8.640 | -5.727 | -2.803 | 1.445 | 1.063 | 2.173 | 1.980 | -1.929 | -2.717 | -0.450 |
| 11 | -64.761 | -50.818 | 2.196 | -9.272 | -12.094 | 0.615 | 0.593 | 1.870 | 2.324 | 3.188 | 1.526 | 1.009 | 3.088 |
| 12 | -68.797 | -52.801 | 0.712 | -8.430 | -6.441 | 2.140 | 0.398 | 2.069 | 2.026 | 0.724 | 1.715 | -0.268 | 0.725 |
| 13 | -67.070 | -57.691 | 4.079 | -7.627 | -6.656 | -2.388 | -2.193 | -1.457 | 2.654 | 4.594 | 1.064 | 1.558 | 3.697 |
| 14 | -63.204 | -60.329 | -0.783 | -12.126 | -13.913 | -10.426 | -1.648 | 1.546 | -2.268 | 3.003 | 4.350 | -4.372 | 0.337 |
| 15 | -61.749 | -60.104 | -2.259 | -8.640 | -6.072 | -2.335 | 1.580 | 0.421 | -0.451 | 1.244 | -0.682 | -2.551 | -3.528 |
| 16 | -59.701 | -53.818 | -1.713 | -8.944 | -11.393 | -5.488 | 1.591 | 1.150 | 2.175 | -0.404 | 1.979 | -1.483 | -0.296 |
| 17 | -54.643 | -55.298 | -7.180 | -10.801 | -10.501 | -1.316 | 3.031 | 2.901 | -0.468 | -0.385 | 3.052 | -2.538 | -2.586 |
| 18 | -51.996 | -54.282 | -6.788 | -11.559 | -3.813 | -7.531 | -0.045 | -1.870 | -2.358 | 1.667 | -0.571 | -0.498 | 0.586 |
| 19 | -47.938 | -52.046 | -8.799 | -12.181 | -12.693 | -8.973 | -0.286 | 1.462 | -1.973 | 4.162 | 3.661 | -0.950 | -0.675 |
| 20 | -54.073 | -45.529 | -1.579 | -6.090 | -13.352 | -9.212 | 3.667 | 5.096 | -2.889 | -3.497 | -0.128 | -3.200 | -3.036 |
| 21 | -44.500 | -13.196 | 6.911 | -1.505 | -5.380 | -10.804 | 1.867 | 1.111 | -6.114 | -3.165 | -0.386 | -4.764 | 1.208 |
| 22 | 10.939 | 8.281 | -11.060 | -10.537 | -7.030 | -13.155 | 0.460 | 0.896 | -3.942 | -3.485 | -3.573 | -3.913 | -1.956 |
| 23 | 32.596 | -4.224 | -12.394 | -13.728 | -6.199 | -13.283 | -3.092 | 5.254 | -4.413 | -6.222 | -2.737 | -2.436 | -1.954 |
| 24 | 31.060 | -2.636 | -8.457 | -20.845 | -6.658 | -7.516 | -10.579 | 8.323 | -2.906 | -6.316 | -5.256 | -1.880 | 0.650 |
| 25 | 29.661 | 0.514 | -8.408 | -25.574 | -1.311 | -0.314 | -15.937 | 8.631 | -0.984 | -5.522 | -8.682 | -1.518 | 4.536 |
| 26 | 25.615 | 2.361 | -10.610 | -26.771 | 0.671 | 1.439 | -15.957 | 12.016 | -5.455 | -2.977 | -5.927 | -2.258 | 2.603 |
| 27 | 19.973 | 2.203 | -10.316 | -28.870 | -2.639 | 1.115 | -13.998 | 9.789 | -7.097 | 3.087 | -4.951 | -2.216 | 2.303 |
| 28 | 9.436 | 5.840 | -11.957 | -37.355 | -1.369 | 1.719 | -13.554 | 7.657 | -3.748 | 4.033 | -1.986 | 1.356 | 2.989 |
| 29 | 9.146 | 16.361 | -10.860 | -33.274 | 0.107 | 6.190 | -6.977 | 0.676 | -3.818 | 0.382 | -4.042 | -3.915 | 1.445 |
| 30 | 17.490 | 7.615 | -9.744 | -32.910 | 4.054 | 9.422 | -7.651 | 2.823 | -5.391 | 2.916 | -4.786 | -5.969 | 0.914 |
| 31 | 3.992 | 3.183 | -12.607 | -43.151 | -3.386 | 2.429 | -8.197 | -0.504 | -7.460 | 2.286 | -2.254 | -5.539 | -0.098 |
| 32 | 3.799 | 7.630 | -12.942 | -37.780 | 0.484 | 5.422 | -6.598 | -3.043 | -6.092 | 1.890 | -3.919 | -6.462 | 0.361 |
| 33 | 1.741 | 8.624 | -6.672 | -35.705 | -1.732 | 5.926 | -3.015 | 1.736 | -5.107 | 2.008 | -3.003 | -4.846 | -0.786 |
| 34 | -9.919 | 3.179 | -15.739 | -36.457 | -3.975 | 4.729 | -2.200 | 2.849 | -3.383 | 2.000 | 0.109 | 0.085 | 2.412 |
| 35 | -15.646 | 8.968 | -8.959 | -33.854 | 1.472 | 9.122 | 1.843 | 3.937 | -3.870 | 1.170 | -1.108 | -5.017 | -1.938 |
| 36 | -20.836 | 15.396 | -11.368 | -38.449 | 3.036 | 6.562 | -6.068 | -2.413 | -4.966 | -0.969 | -7.324 | -3.543 | -1.175 |
| 37 | -26.521 | 13.695 | -11.808 | -35.462 | 3.098 | 8.545 | -4.209 | 0.126 | -3.227 | -1.414 | -6.059 | -2.327 | -0.107 |
| 38 | -37.598 | 5.751 | -17.405 | -36.898 | 3.517 | 4.346 | -3.525 | 3.940 | -2.532 | 1.085 | -4.538 | -1.043 | 2.290 |
| 39 | -44.037 | 4.908 | -5.998 | -33.543 | 6.719 | 4.484 | -0.873 | 3.632 | -1.912 | 3.161 | -2.066 | -2.119 | 0.506 |
| 40 | -54.880 | 14.961 | -5.015 | -30.692 | 9.378 | 2.551 | -6.917 | -0.244 | -3.498 | 4.220 | -5.074 | -1.149 | -0.330 |
| 41 | -50.737 | 18.469 | -7.010 | -26.559 | 5.575 | 4.381 | -4.626 | 2.512 | -4.038 | 2.283 | -6.958 | -3.240 | -0.381 |
| 42 | -79.521 | 13.416 | -6.584 | -25.720 | 2.132 | 8.239 | -2.727 | 3.353 | -2.931 | -0.800 | -5.412 | -0.427 | 3.383 |
| 43 | -82.772 | 18.596 | -4.013 | -18.647 | 5.185 | 7.213 | 0.271 | 1.833 | -1.365 | -0.187 | -3.130 | 0.401 | 0.647 |
| 44 | -87.535 | 19.907 | -3.356 | -20.160 | -5.426 | -1.762 | -1.774 | 5.000 | 0.684 | -1.017 | -2.955 | 0.367 | 1.294 |
| 45 | -94.737 | 19.109 | -3.676 | -16.580 | 3.534 | 6.083 | -1.064 | -2.777 | -6.796 | -4.260 | -4.687 | 2.547 | 2.741 |
| 46 | -100.118 | 21.012 | -3.546 | -16.181 | 0.048 | 6.209 | -0.702 | 6.520 | -5.159 | -2.413 | -4.863 | -1.805 | -0.625 |
| 47 | -107.109 | 19.482 | -4.193 | -16.937 | 1.714 | 1.714 | -7.896 | -3.074 | -3.345 | 1.195 | -2.037 | -0.186 | -0.128 |
| 48 | -114.674 | 20.465 | -9.934 | -9.570 | 5.330 | 7.618 | 4.003 | -2.378 | -10.432 | -1.421 | -2.696 | 0.462 | 2.127 |
| 49 | -122.764 | 16.336 | -10.797 | -11.067 | 1.057 | 2.650 | -0.685 | -2.364 | -8.969 | -0.321 | -5.542 | -0.868 | 0.691 |
| 50 | -118.829 | 16.269 | -3.310 | -1.799 | 5.975 | 0.537 | -1.193 | -0.224 | -9.996 | 3.418 | -4.118 | -1.198 | -0.648 |
| 51 | -128.750 | 19.342 | -7.934 | -8.196 | 1.346 | 2.066 | -3.675 | 3.006 | -8.899 | 0.076 | -6.086 | 1.114 | 2.204 |
| 52 | -125.066 | 14.624 | -4.327 | -2.610 | -1.293 | 2.212 | 0.614 | 1.074 | -2.920 | -4.057 | -4.420 | -0.355 | 3.185 |
| 53 | -63.111 | -9.510 | 10.596 | -13.107 | -13.977 | -0.802 | -0.894 | 0.088 | -4.749 | 2.264 | -1.841 | -2.590 | -0.605 |
| 54 | -75.429 | -6.416 | -8.053 | -13.452 | -7.041 | -5.357 | 0.200 | 5.779 | -1.239 | 5.943 | 0.409 | -1.878 | -0.257 |
| 55 | -102.627 | -10.736 | -5.331 | -2.975 | 0.717 | -2.020 | -0.730 | -1.294 | -3.260 | -2.508 | 0.068 | -1.186 | -3.313 |
| 56 | -91.079 | -11.605 | -13.268 | -4.555 | 7.649 | -1.049 | 1.801 | 1.114 | -2.578 | 3.295 | -1.534 | -1.702 | -3.832 |
| 57 | -90.934 | -8.823 | -7.553 | -9.166 | 2.696 | -2.614 | -0.105 | -3.861 | -5.866 | -0.505 | -6.371 | -0.657 | -1.076 |
| 58 | -90.366 | -15.204 | -23.178 | -12.567 | -3.657 | -5.083 | 2.840 | 1.356 | -3.565 | 3.116 | -2.158 | -4.485 | 0.072 |
| 59 | -94.910 | -5.865 | -9.891 | -4.758 | -1.676 | -3.209 | 2.390 | 0.711 | -6.012 | 0.002 | -3.331 | -3.450 | 0.867 |
| 60 | -108.855 | -6.600 | -20.903 | -19.265 | -11.843 | -8.288 | -2.796 | -0.791 | -3.762 | -0.621 | -4.780 | -5.844 | -1.353 |
| 61 | -110.043 | 1.888 | -8.338 | -10.473 | -2.708 | 2.267 | 7.620 | -1.592 | -2.277 | 1.735 | -5.547 | -1.750 | -0.975 |
6 运行代码
6.1 安装
配置环境前,首先需要安装以下依赖:
- Anaconda 2022.05 或以上(含 Python 3.9)
然后创建并激活 conda 虚拟环境,同时安装所有依赖包:
6.2 使用
将音频文件放置于 ./data/dev_set 目录下,执行以下命令启动程序:
|
|
生成的语音波形图、MFCC 系数以及过程中产生的其他图像将保存在 ./assets/mfcc 目录下。
6.3 测试
本实验中,我们使用了预录制的音频文件 shop.dat,其内容是单词 shop 的一段语音,按 8000 Hz 采样。
运行程序后,程序将在 ./assets/mfcc 目录下生成以下文件:
foobar_time_domain.png:原音频foobar.dat的语音波形图,包括检测到的语音段范围foobar_zcr.png:信号的过零率(ZCR)曲线mel_filters_n_fmin-fmax.png:窗口宽度为 $N$,频率范围为 $[f_{\min}, f_{\max}]\ \mathrm{Hz}$ 的 Mel 滤波器组foobar_spectrogram_tms_hamming.png:信号在 $t\ \mathrm{ms}$ 窗口宽度下的语谱图foobar_power_spec_tms_hamming_filtered.png:信号经 Mel 滤波器组处理后的能量图foobar_mfcc.txt:利用离散余弦变换(DCT)得到的 Mel 频率倒谱系数(MFCC)foobar_mfcc.png:上述 MFCC 系数的可视化图像